- Home
- Physics
- Philosophy
- NATO-Ukraine-Russia War
- Politics
- Salem City Council minutes 1998-1999
- Mangala talk on Sufism
- Amar Kumar on the Koran
- Amar Kumar on Castes in India
- Amar Kumar on Gandhi
BROWNIAN MOTION
Brownian motion is the irregular and rapid motion of particles invisible to the naked eye but large enough to be seen in an ordinary visible-light microscope. The motion is technically a “random walk,” or more picturesquely a “drunkard’s walk” in which the particle seems to undergo a zig-zag motion as shown in the following figure.
A Brownian particle is huge compared to an atom. For example, a particle barely visible in an ordinary optical microscope consists of trillions of atoms. Figure 1 illustrates the positions a particle would be observed at, starting at the dot at the bottom, and ending at the upper dot, the positions being observed periodically, e.g., every 30 seconds or so.
A Brownian particle is huge compared to an atom. For example, a particle barely visible in an ordinary optical microscope consists of trillions of atoms. Figure 1 illustrates the positions a particle would be observed at, starting at the dot at the bottom, and ending at the upper dot, the positions being observed periodically, e.g., every 30 seconds or so.
Brownian motion is named after Robert Brown, who carefully investigated the phenomenon in the early 1800s. The great historical importance of the phenomenon is that its explanation and experimental verification conclusively proved that atoms exist.
The explanation was provided by Albert Einstein in 1905, at a time when the existence of atoms was widely but not universally accepted. Einstein assumed that the particles are no different than atoms, except that the particles are much bigger but exhibit the random thermal motion atoms were believed to have. He derived an equation that predicted how far a particle should wander over a time t from its starting position. This “wandering distance” depends on such things as the temperature of the fluid the particles are suspended in (usually water), the viscosity of the fluid which determines the drag of the fluid on particle motion (for example, molasses is much more viscous than water), and the size of the particle. Specifically, he predicted that the wandering distance is proportional to the square root of the time. So a particle moves from its starting point only about two times as far in 120 seconds as it does in 30 seconds, even though it is traveling for four times as long. The reason the wandering distance isn’t directly proportional to the time is that the random zigs and zags cause the particle to occasionally decrease its distance from the starting point, even though on average it will wander farther away. Put another way, the total distance traveled is greater than the simple total displacement from the starting point because of all the zigs and zags, as can be verified by adding the lengths of all the legs in the figure compared to the straight-line distance between the start and end dots.
Einstein’s prediction of the wandering distance was experimentally verified in a series of painstaking experiments by Jean Perrin, who published his work in 1912. After that, no one seriously doubted the existence of atoms.
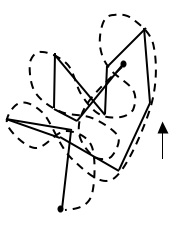
It is important to understand the space and time scales over which Brownian motion occurs. The zig-zag motion shown in Figure 1 is “self-similar” in the sense that more frequent observations of the particle would show the motion to be similarly irregular but with smaller distance between zig and zag points. This is illustrated in Figure 2 for the bottom-right leg of the path shown in Figure 1:
The explanation was provided by Albert Einstein in 1905, at a time when the existence of atoms was widely but not universally accepted. Einstein assumed that the particles are no different than atoms, except that the particles are much bigger but exhibit the random thermal motion atoms were believed to have. He derived an equation that predicted how far a particle should wander over a time t from its starting position. This “wandering distance” depends on such things as the temperature of the fluid the particles are suspended in (usually water), the viscosity of the fluid which determines the drag of the fluid on particle motion (for example, molasses is much more viscous than water), and the size of the particle. Specifically, he predicted that the wandering distance is proportional to the square root of the time. So a particle moves from its starting point only about two times as far in 120 seconds as it does in 30 seconds, even though it is traveling for four times as long. The reason the wandering distance isn’t directly proportional to the time is that the random zigs and zags cause the particle to occasionally decrease its distance from the starting point, even though on average it will wander farther away. Put another way, the total distance traveled is greater than the simple total displacement from the starting point because of all the zigs and zags, as can be verified by adding the lengths of all the legs in the figure compared to the straight-line distance between the start and end dots.
Einstein’s prediction of the wandering distance was experimentally verified in a series of painstaking experiments by Jean Perrin, who published his work in 1912. After that, no one seriously doubted the existence of atoms.
It is important to understand the space and time scales over which Brownian motion occurs. The zig-zag motion shown in Figure 1 is “self-similar” in the sense that more frequent observations of the particle would show the motion to be similarly irregular but with smaller distance between zig and zag points. This is illustrated in Figure 2 for the bottom-right leg of the path shown in Figure 1:
You might think that observation at even smaller times would show each of the extra legs shown in the figure to be really a number of random smaller legs. This is true as long as the time between observations is not below the “time scale” of the motion. At very small times below the time scale, the motion becomes smooth, as shown in Figure 3 which shows the true continuous motion of the particle (dashed path) superimposed on the zig-zag motion shown in Figure 1:
To download a primer on Brownian motion, written at an elementary level (involving a bit of algebra and some optional calculus), click on this link:
| snapshots_of_brownian_motion_primer.pdf | |
| File Size: | 2186 kb |
| File Type: | |
A space scale of the motion is associated with the time scale. Since distance equals speed times time, the space scale is simply the average thermal speed of the particle times the time scale. An eyeball guess of the space scale is represented in the Figure 3 by the vertical arrow on the lower-right. It is roughly how far the particle travels in its continuous path before substantially changing direction.
Here are some typical numerical values of time and space scales and other important physical parameters. Consider a Brownian particle of radius 0.000001 meter (about 1/100th the thickness of a human hair, or in powers of 10, 10^-6 or “ten to the minus 6” meter), barely visible under a standard visible-light microscope. Assuming its density is the same as water’s, its mass is 4.2x10^-15 kilograms. Its average thermal speed at room temperature (taken for convenience as 27 deg Celsius) is 0.00172 m/s, or if you wish, about 1/16th of an inch per second. In water, its time scale is about 2.23x10^-7 seconds, and the space scale is a tiny 3.84x10^-10 m, not much bigger than the diameter of a typical atom! So it takes only this short distance and short time for the particle to substantially change its direction. In air, the time scale is 1.23x10^-5 s, and the space scale is 2.12x10^-8 m (about 200 times the diameter of a typical atom). Clearly, Perrin, who marked changes in the particle’s position manually, could not track on short enough a time-scale to see smooth motion. He typically recorded the positions of particles at 30-second intervals.
If you are interested in a more technical treatment of time and space scales in Brownian motion, click on this link:
Here are some typical numerical values of time and space scales and other important physical parameters. Consider a Brownian particle of radius 0.000001 meter (about 1/100th the thickness of a human hair, or in powers of 10, 10^-6 or “ten to the minus 6” meter), barely visible under a standard visible-light microscope. Assuming its density is the same as water’s, its mass is 4.2x10^-15 kilograms. Its average thermal speed at room temperature (taken for convenience as 27 deg Celsius) is 0.00172 m/s, or if you wish, about 1/16th of an inch per second. In water, its time scale is about 2.23x10^-7 seconds, and the space scale is a tiny 3.84x10^-10 m, not much bigger than the diameter of a typical atom! So it takes only this short distance and short time for the particle to substantially change its direction. In air, the time scale is 1.23x10^-5 s, and the space scale is 2.12x10^-8 m (about 200 times the diameter of a typical atom). Clearly, Perrin, who marked changes in the particle’s position manually, could not track on short enough a time-scale to see smooth motion. He typically recorded the positions of particles at 30-second intervals.
If you are interested in a more technical treatment of time and space scales in Brownian motion, click on this link:
| fluctuation_and_relaxation_time_in_brownian_motion_27_may_2010.pdf | |
| File Size: | 929 kb |
| File Type: | |
For those who want to start with a complete treatment of Brownian motion, here is my paper on the necessary role of pressure fluctuations in fluids like air and water and the inappropriate use of the well-known Wiener process for the fluctuation component of the Langevin equation:
| pressure_fluctuations_viscosity_and_brownian_motion_arxiv_rev.pdf | |
| File Size: | 5029 kb |
| File Type: | |